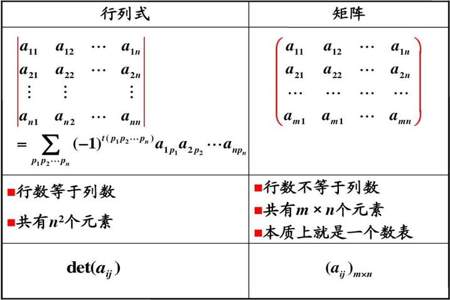
矩阵和行列式都是线性代数中的基本概念,它们之间有很多联系。矩阵是一个n*m的数表,而行列式是一个n阶的方阵。矩阵不能从整体上被看成一个数,而行列式最终可以算出来变成一个数。矩阵的加减和乘法规律都和行列式的不同 。
矩阵和行列式的区别
矩阵和行列式是线性代数中的重要概念,它们在求解线性方程组、变换矩阵等问题中起着关键作用。虽然它们都涉及到元素的排列组织,但它们的定义、性质和用途略有不同。
首先,让我们来看看矩阵。矩阵是由数个数值按照规则排列成的一个矩形阵列。它可以是1行m列的行向量,也可以是n行1列的列向量,还可以是n行m列的矩阵。它的元素可以是实数、复数或其他代数结构的元素。矩阵可以用来表示线性变换、向量空间以及解线性方程组等。
行列式则是一个与矩阵相关的标量量值。对于一个n阶方阵,行列式可以用一种特殊的方式来计算。它是由矩阵的元素按某种规则排列并通过加减运算得到的。行列式可以表示出矩阵的一些重要性质,例如对角化、可逆性等。在求解线性方程组、矩阵的特征值和特征向量等问题中,行列式的计算往往起到关键作用。
简而言之,矩阵是一个按规则排列的矩形阵列,用于表示线性变换和求解线性方程组等问题;而行列式是通过对矩阵的元素进行特定运算得到的标量量值,用于表达矩阵的一些重要性质。它们都是线性代数中不可或缺的概念,相辅相成,相互补充。
矩阵和行列式的区别
矩阵和行列式是线性代数中的两个概念,它们有一些相同之处,但也有一些主要的区别。
首先,矩阵是由数字按照规则排列形成的一个矩形数组。
它可以有任意多的行和列,由 [行数, 列数] 表示。
矩阵中的每个元素可以是实数、复数或其他代数结构。
矩阵主要用于表示线性方程组和线性变换。
而行列式则是一个数值,它是一个关于矩阵的特定函数。
行列式的值可以通过一种特定的计算方法得到。
行列式的计算结果可以提供关于矩阵性质的信息,如是否可逆、线性无关等。
从定义上看,矩阵是一个具体的结构,而行列式是与矩阵相关的一个数学工具。
矩阵中的元素可以用于进行各种运算,如矩阵相加、相乘等。
而行列式则是对矩阵的一种特定计算,它可以用于判断矩阵的性质或与其他矩阵进行比较。
所以,矩阵在形式上更加灵活,可以进行各种操作,而行列式则是一种特定的计算方法和结果。
它们在线性代数中有着不同的用途和意义。
矩阵和行列式的区别
1、定义不同
行列式
在数学中,是一个函数,其定义域
为det的矩阵A,取值为一个标量。
在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵。
2、表达式不同
行列式:n阶行列式
设
是由排成n阶方阵形式的n²个数aij(i,j=1,2,...,n)确定的一个数,其值为n!项之和。
矩阵:由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。记作:
这m×n 个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n,m×n矩阵A也记作Amn。
3、性质不同
行列式:行列式A中某行(或列)用同一数k乘,其结果等于kA。
行列式A等于其转置行列式AT(AT的第i行为A的第i列)。
若n阶行列式|αij|中某行(或列);行列式则|αij|是两个行列式的和,这两个行列式的第i行(或列),一个是b1,b2,…,bn;另一个是с1,с2,…,сn;其余各行(或列)上的元与|αij|的完全一样。
行列式A中两行(或列)互换,其结果等于-A。 ⑤把行列式A的某行(或列)中各元同乘一数后加到另一行(或列)中各对应元上,结果仍然是A。
矩阵:对称矩阵A正定的充分必要条件
是A的n个特征值全是正数。
对称矩阵A正定的充分必要条件是A合同于单位矩阵
E。
对称矩阵A正定(半正定)的充分必要条件是存在n阶可逆矩阵
U使A=U^TU
对称矩阵A正定,则A的主对角线元素均为正数。
对称矩阵A正定的充分必要条件是:A的n个顺序主子式
全大于零。
矩阵和行列式的区别
行列式是若干数字组成的一个类似于矩阵的方阵,与矩阵不同的是,矩阵的表示是用中括号,而行列式则用线段.矩阵由数组成,或更一般的,由某元素组成.
行列式的值是按下述方式可能求得的所有不同的积的代数和,即是一个实数求每一个积时依次从每一行取一个元因子,而这每一个元因子又需取自不同的列,作为乘数,积的符号是正是负决定于要使各个乘数的列的指标顺序恢复到自然顺序所需的换位次数是偶数还是奇数.也可以这样解释:行列式是矩阵的所有不同行且不同列的元素之积的代数和,和式中每一项的符号由积的各元素的行指标与列指标的逆序数之和决定:若逆序数之和为偶数,则该项为正;若逆序数之和为奇数,则该项为负.
矩阵和行列式的区别
矩阵和行列式是线性代数中的常见概念,它们有一些相似之处,但也有一些区别。
矩阵是一个由数字或符号排列成的矩形阵列。它由行和列组成,其中每个元素可以是实数、复数或其他可操作的对象。矩阵通常用大写字母表示,如A、B、C等。矩阵可以进行加法、减法和乘法运算,可以进行矩阵的转置、逆运算等。
行列式是一个由数字组成的正方形阵列,它由行和列组成。行列式通常用竖线或方括号表示,如|A|或[A]。行列式的值是一个标量,它是一个表示线性变换的重要参数。行列式在线性方程组的求解、矩阵的特征值和特征向量等方面具有重要作用。
所以,矩阵是一个更广义的概念,它可以用来表示各种各样的数学对象,而行列式是一种特定类型的矩阵,具有特定的数学属性和用途。
矩阵和行列式的区别
矩阵和行列式都是线性代数中的重要概念,但它们有不同的定义和用途:
1. 矩阵(Matrix):
- 矩阵是一个二维的数学结构,通常由行和列组成。
- 矩阵的元素可以是实数、复数或其他数域中的数值。
- 矩阵常用于表示线性方程组、线性变换和向量空间的基。
- 一个 m×n 矩阵有 m 行和 n 列,通常表示为 A=[a_ij],其中 a_ij 表示矩阵 A 的第 i 行第 j 列的元素。
2. 行列式(Determinant):
- 行列式是一个与方阵相关的标量值,用于描述方阵的性质。
- 行列式只适用于方阵,即行数和列数相等的矩阵。
- 行列式的值表示了方阵的线性变换对体积伸缩的影响,它可以用于判断方阵是否可逆,以及计算线性方程组的解的数量。
- 一个 n 阶方阵的行列式通常表示为 |A|。
总之,矩阵是一个具有行和列的二维数学结构,而行列式是一个与方阵相关的数值,用于描述方阵的性质和影响。在线性代数中,它们经常一起使用,以便解决线性方程组和研究线性变换的性质。
矩阵和行列式的区别
1、本质上,矩阵是一个数表,行列式是一个数值,n阶的方阵。
2、数字符号上,矩阵是用括号表示的,行列式是用双竖线表示的。
3、结构上,矩阵的行数和列数可以不一样,行列式的行数与列数一致。
4、运算上,一个数乘以行列式,只能乘以行列式的一行或者一列。一个数乘以矩阵,矩阵的每个元素都要乘上这个数。两个矩阵相等是指对应元素都相等;两个行列式相等不要求对应元素都相等,甚至阶数也可以不一样,只要运算代数和的结果一样就行了。
行列式相等,就是值相等,行和列数目不必相等,数据也不必相等。矩阵相等,行和列数目必须相等,对应位置的数据也必须相等。行列式相加减,就是两个数值相加减,结果还是数值。矩阵相加减,对应位置的数据相加减。
矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中,行列式可以看做是有向面积或体积的概念在一般的欧几里得空间中的推广。
矩阵和行列式的区别
1、本质上,矩阵是一个数表,行列式是一个数值,n阶的方阵。
2、数字符号上,矩阵是用括号表示的,行列式是用双竖线表示的。
3、结构上,矩阵的行数和列数可以不一样,行列式的行数与列数一致。
矩阵和行列式的区别
答:
矩阵和行列式的区别如下:
1. 矩阵是一个表格,行数和列数可以不一样;而行列式是一个数,且行数必须等于列数。只有方阵才可以定义它的行列式,而对于长方阵不能定义它的行列式。
2. 两个矩阵相等是指对应元素都相等;两个行列式相等不要求对应元素都相等,甚至阶数也可以不一样,只要运算代数和的结果一样就行了。
3.两矩阵相加是将各对应元素相加;两行列式相加,是将运算结果相加,在特殊情况下(比如有行或列相同),只能将一行(或列)的元素相加,其余元素照写。
4.数乘矩阵是指该数乘以矩阵的每一个元素;而数乘行列式,只能用此数乘行列式的某一行或列,提公因数也如此。
5.矩阵经初等变换,其秩不变;行列式经初等变换,其值可能改变:换法变换要变号,倍法变换差倍数;消法变换不改变。
