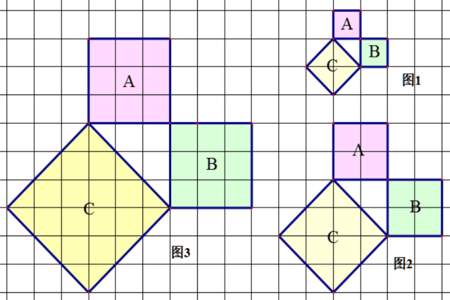
勾股定理的平方怎么来的

设直角三角形abc的三边向量分别为A,B,C

其中A,B为互相垂直的两个向量

有AB=0 (内积公式)

根据完全平方公式

(A+B)^2 = A^2 + 2AB + B^2

= A^2 + B^2

A+B正好是向量C

所以有C^2 = A^2+B^2

勾股定理的平方怎么来的

是从正方形和三角形的面积割补法得来的