如何画无理数的数轴

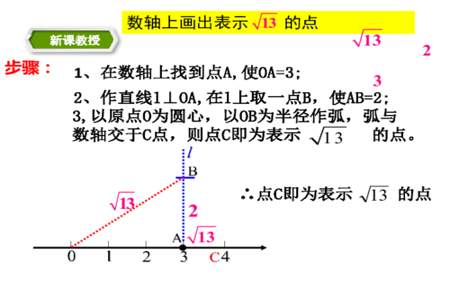
在数轴上表示无理数可以用直角三角形的勾股定理来作图。例如，取一条边是1（数轴上的单位长），作出一个直角，再取另一条边为1，那么所形成的三角形的斜边就是根号2，而根号2就是一个无理数。

无理数，也称为无限不循环小数，不能写作两整数之比。若将它写成小数形式，小数点之后的数字有无限多个，并且不会循环。常见的无理数有非完全平方数的平方根、π和e（其中后两者均为超越数）等。无理数的另一特征是无限的连分数表达式。无理数最早由毕达哥拉斯学派弟子希伯索斯发现。