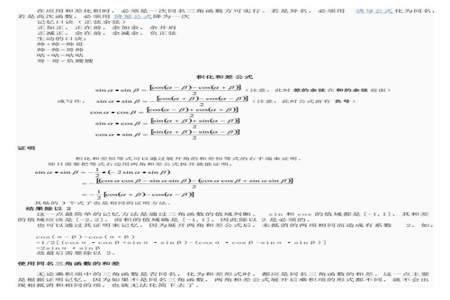
差化积公式推导过程:
已知sin(A+B)=sinAcosB+cosAsinB,sin(A-B)=sinAcosB-cosAsinB,两式相加可得sin(A+B)+sin(A-B)=2sinAcosB。所以,sinAcosB=(sin(A+B)+sin(A-B))/2。同理,两式相减可得cosAsinB=(sin(A+B)-sin(A-B))/2。
同样的,已知cos(A+B)=cosAcosB-sinAsinB,cos(A-B)=cosAcosB+sinAsinB,两式相加可得cos(A+B)+cos(A-B)=2cosAcosB,所以,cosAcosB=(cos(A+B)+cos(A-B))/2。同理,两式相减可得sinAsinB=-(cos(A+B)-cos(A-B))/2。
这样,就得到了积化和差的四个公式。
有了积化和差的四个公式以后,只需一个变形,就可以得到和差化积的四个公式,将上述四个公式中的A+B设为x,A-B设为y,那么A=(x+y)/2,B=(x-y)/2。
把A,B分别用x,y表示就可以得到和差化积的四个公式:
1、sinx+siny=2sin((x+y)/2)cos((x-y)/2);
2、sinx-siny=2cos((x+y)/2)sin((x-y)/2);
3、cosx+cosy=2cos((x+y)/2)cos((x-y)/2);
4、cosx-cosy=-2sin((x+y)/2)sin((x-y)/2)
评论
暂无评论
