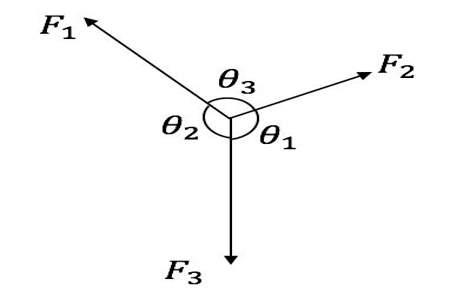
拉密定理是数学中的一个重要定理,它描述了在一个闭区间上连续的实值函数的中间值性质。下面是拉密定理的证明过程:
假设函数 f(x) 在闭区间 [a, b] 上连续,并且 f(a) ≠ f(b)。现在我们定义一个值 y,它介于 f(a) 和 f(b) 之间,即 f(a) < y < f(b) 或 f(b) < y < f(a)。
考虑函数 g(x) = f(x) - y。由于 f(x) 和 y 都是连续函数,所以 g(x) 也是连续函数。根据初等函数的性质,我们知道 g(a) = f(a) - y < 0,而 g(b) = f(b) - y > 0。
根据闭区间 [a, b] 上连续函数的性质,我们可以得出结论:如果 g(a) < 0 且 g(b) > 0,那么在闭区间 [a, b] 内存在至少一个实数 c,使得 g(c) = 0。
换句话说,存在一个实数 c,使得 f(c) - y = 0,即 f(c) = y。由于 f(a) ≠ f(b),所以 y 介于 f(a) 和 f(b) 之间,即 f(a) < f(c) < f(b) 或 f(b) < f(c) < f(a)。
这就证明了拉密定理:对于闭区间 [a, b] 上的连续函数 f(x),如果 f(a) ≠ f(b),那么对于 f(a) 和 f(b) 之间的任意一个值 y,存在至少一个实数 c,使得 f(c) = y。
这个定理的重要性在于它提供了一个基本结果,使得我们可以推断函数在闭区间上取到任意中间值的存在性,为解决各种数学问题提供了有力的工具。
