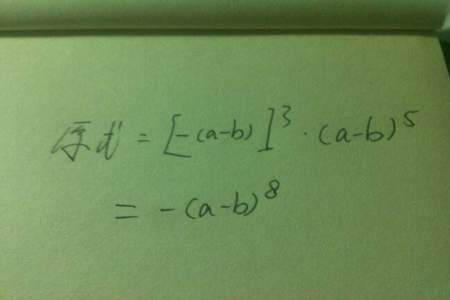
1. 公式为 (a-b)^52. 这个公式是指将 (a-b) 乘以自己五次,即 (a-b) x (a-b) x (a-b) x (a-b) x (a-b),可以用分配律展开,得到一个多项式。
3. 这个公式可以用于计算某些数学问题,例如展开一个五次方的多项式,或者求解某些几何问题中的长度或面积。
a-b的5次方的公式
(a-b)的5次方=(a-b)(a-b)(a-b)(a-b)(a-b)
(a-b)的3次方=(a-b)(a-b)(a-b)
咱们现在还没学到那,所以结果是这个的话,就这样留着就可以了!
a-b的5次方的公式
这题主要考察二项式定理,作物五次方的二项式展开得到结果等于a的五次减a的四次乘以b+a的三次乘以b^2 -a^2×b的三次加a×b的四次减b的五次
a-b的5次方的公式
为(a-b)^5。这个公式可以通过二项式定理来得出,即(a-b)^5 = C(5,0)a^5b^0 - C(5,1)a^4b^1 + C(5,2)a^3b^2 - C(5,3)a^2b^3 + C(5,4)a^1b^4 - C(5,5)a^0b^5,其中C(n,k)表示从n个元素中选取k个元素的组合数。这个公式可以用来求解a-b的5次方,其中a和b可以是任意实数。
a-b的5次方的公式
$a-b$ 的五次方可以使用二项式定理进行展开,即:
$$(a-b)^5=\sum_{k=0}^5\binom{5}{k}a^{5-k}(-b)^k$$
其中,$\binom{5}{k}$ 表示从 5 个元素中取 $k$ 个元素的组合数。
将 $\binom{5}{k}$ 和 $(-1)^k$ 相乘,可以得到公式的另一种形式:
$$(a-b)^5=\sum_{k=0}^5(-1)^k\binom{5}{k}a^{5-k}b^k$$
根据以上公式,$a-b$ 的五次方的展开式为:
$$ (a-b)^5 = a^5-5a^4b+10a^3b^2-10a^2b^3+5ab^4-b^5 $$
这就是 $(a-b)^5$ 的公式。
