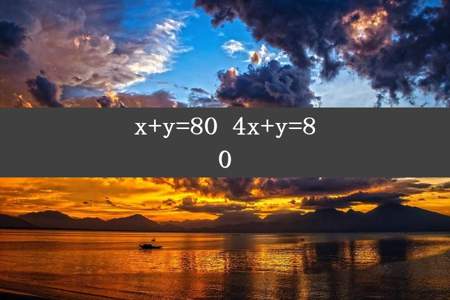
这是一道二元一次等式求解问题,解题方式如下:
首先列方程组
x+y=80
4x+y=80
相减即得3x=0
所以x=0
代入得y=80
所以答案为x=0 y=80
x+y=80 4x+y=80
x=0 y=80
已知X+Y=80,且4XY+800=6400即
XY=1400所以X=1400/Y
将其待入X+Y=80得1400/Y+Y=80
,即1400+Y^2=80Y
即 (Y-40)^2=1600-1400=200
所以Y=40±10√2待入X+Y=80
得当Y=40+10√2时
X=80-Y=40-10√2
或当Y=40-10√2时 X=80-Y=0
x+y=80 4x+y=80
4(x+y)=80 5(x-y)=80
x+y=80/4=20
x-y=80/5=16
(x+y)+(x-y)=2x=20+16=36
x=18
y=20-x20-18=2
x=18 y=2
