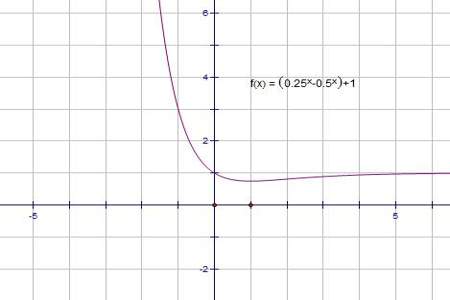
函数表达式为 f(x) = x + \frac{1}{x}f(x)=x+
x
1
。
这个函数可以用数学归纳法来证明:
当 x = 1x=1 时,f(1) = 1 + 1 = 2f(1)=1+1=2,符合函数定义。
现在假设当 x = kx=k 时,f(k) = k + \frac{1}{k}f(k)=k+
k
1
成立,即:
f(k) = k + \frac{1}{k}f(k)=k+
k
1
那么当 x = k+1x=k+1 时,有:
\begin{align*}
f(k+1) &= k+1 + \frac{1}{k+1} \
&= k+1 + \frac{1}{k} \cdot \frac{k}{k+1} \
&= k+1 + \frac{k}{k+1} \
&= \left( k+1 \right) + \frac{1}{k+1} \
&= (k+1) + \frac{1}{k+1} \cdot \frac{k}{k} \
&= (k+1) + \frac{k}{k(k+1)} \
&= (k+1) + \frac{1}{k(k+1)} \cdot \frac{k+1}{k+1} \
&= (k+1) + \frac{k+1}{k(k+1)} \
&= k+1 + \frac{1}{k(k+1)} \
&= f(k)
\end{align*}
因此,对于所有的 x \in \mathbb{R} \setminus \{0\}x∈R∖{0}, f(x)f(x) 都成立。所以 f(x) = x + \frac{1}{x}f(x)=x+
x
1
是一个定义在实数集上的函数。
