有理数和无理数是什么概念

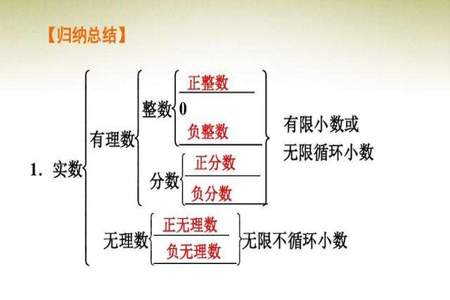
有理数和无理数是数学中的两个基本概念。

有理数是指可以表示为两个整数之比的数，即可以表示为 m/n 的形式，其中 m 和 n 都是整数，且 n 不等于 0。有理数也被称为可分数，包括整数和分数。例如，2/3、-4/5、1/2、2/1 等都是有理数。

无理数是指不能表示为两个整数之比的数，也就是无法用有限的小数或循环小数来表示的数。无理数也被称为不可分数，例如 π（圆周率）、e（自然对数的底数）以及一些超越数（如黄金分割数）等都是无理数。

需要注意的是，0 既不是有理数，也不是无理数。因为 0 不能作为分母，所以无法表示为两个整数之比。但是 0 是一个有理数的特殊情况，即 0/1 = 0。

另外，有理数和无理数的概念是建立在实数的基础上的。有理数可以与实数建立一一对应的关系，即实数中的每一个有理数都可以表示为两个整数之比，因此有理数在实数中是稠密的，即任意两个有理数之间都有无数个有理数。无理数在实数中也是稠密的，但无理数的个数比有理数多得多，因为存在许多超越数，例如 π 和 e 等，这些超越数的个数是无限的。

有理数和无理数是什么概念

有理数和无理数是数学中常见的两个数的分类概念。

有理数是可以表示为两个整数的比值的数，或者是可以表示为有限小数或循环小数的数。有理数包括整数、分数、有限小数和循环小数。例如，1/2，3，-5和0.75都是有理数。

无理数是不能表示为两个整数的比值的数，也不能表示为有限小数或循环小数的数。无理数的十进制表示是无限不循环的。无理数包括无限不循环小数和无限不循环小数的平方根、立方根等根式。例如，根号2 (√2)、π (pi)和自然对数的底数e都是无理数。

有理数和无理数一起构成了实数的完整集合。无理数的存在使得实数可以填补有理数中可能存在的空隙。无理数的表示通常使用根号 (√)和其他特殊符号，而有理数可以直接用分数或小数表示。

需要强调的是，有理数和无理数是根据其表示形式以及能否被表示为比值或有限循环小数来分类的，与数的大小无关。无理数也可以是无限大或无限小的数。

有理数和无理数是什么概念

把有理数和无理数都写成小数形式时，有理数能写成有限小数和无限循环小数。

比如4=4.0, 4/5=0.8, 1/3=0.33333……而无理数只能写成无限不循环小数,

比如√2=1.414213562…………根据这一点,人们把无理数定义为无限不循环小数.

所有的有理数都可以写成两个整数之比;而无理数不能。根据这一点，有人建议给无理数摘掉“无理”的帽子，把有理数改叫为“比数”，把无理数改叫为“非比数”。本来嘛，无理数并不是不讲道理，只是人们最初对它不太了解罢了。

有理数和无理数是什么概念

回 有理数和无理数是数学中的概念。

1. 有理数是指可以表示为两个整数的比例的数，它们可以用分数的形式表示，例如1/2、3/4等。

有理数具有有穷的小数或循环小数表示形式，可以用分数的形式精确表示。

2. 无理数是指不能表示为两个整数的比例的数，它们的小数表示形式无限不循环，例如√2、π等。

无理数无法被准确表示为分数或有限小数。

总结：有理数是可以用分数或有穷循环小数表示的数，而无理数无法用分数或有限小数表示，它们在数学中有着不同的特征和性质。

有理数和无理数是什么概念

有理数是指两个整数的比，包括整数和分数，其小数部分是有限或无限循环的数。0也是有理数。不是有理数的实数称为无理数，即无限不循环小数的数1。 无理数包括无限不循环小数和开根开不尽的数2。 有理数和无理数是数学中的重要概念，有广泛的应用，是继续学习实数、代数式、方程、不等式、直角坐标系、函数、统计等数学内容以及相关学科知识的基础