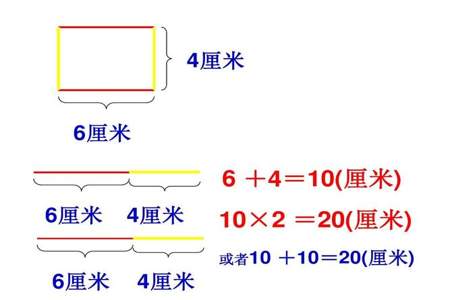
答:因为在同一周长的情况下,正方形具有最大的对称性。在其他形状的情况下,存在一些角落会浪费周长。而正方形存在四个相等的边,使得周长均匀分布,能够最好地利用周长去填充面积。
同时,正方形也是在同一条件下拥有最大面积的多边形,因此在同一周长的长方形内,正方形的面积也会最大化。
周长一样为什么正方形最大
正方形是一种特殊的矩形,它的四条边长度相等。在给定周长的情况下,正方形具有最大的面积。
我们知道,矩形的面积等于长乘以宽。当矩形的周长一定时,它的长和宽的和最大,才能使得面积最大。
假设矩形的周长是L,长为x,宽为y,则有L = 2x + 2y。为了使x+y的值最大,我们可以使用一些数学技巧,例如求解最优化问题或者利用导数的方法等。但实际上,当L固定时,无论如何排列长和宽,只有在x=y时长和宽的和才能得到最大值。
而正方形的特点是四条边长度相等,也就是x=y,因此它是在给定周长下面积最大的矩形。
简言之,正方形以其特殊的边长关系,即四边相等,达到了在给定周长下最大化面积的目标。
周长一样为什么正方形最大
正方形是一种特殊的矩形,它的四条边长度相等,且四个角都是直角。由于周长是一个形状的边界长度,而正方形的四条边长度相等,所以正方形的周长最大。对于给定的面积,正方形也是能够包含最大面积的矩形形状。这是因为正方形的四条边长度相等,所以它的面积最大。
