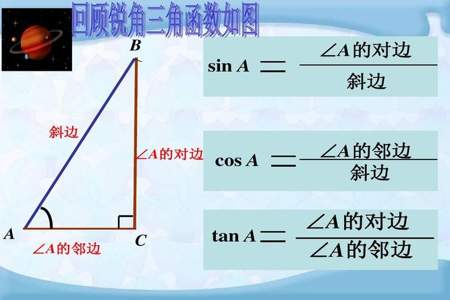
三角函数是一种用于计算三角形内角和边长关系的数学工具。如果我们已知一个右角三角形中的一个角和与之相邻的边长,我们就可以使用三角函数来计算该三角形的其他边长。其中,求三角形斜边(即斜边长)的方法如下:
假设已知一个直角三角形,其中直角所对应的角度为 $90^{\circ}$,另外两个角度所对应的为 $\alpha$ 和 $\beta$,斜边长为 $c$,而另外两边长为 $a$ 和 $b$,则有以下三个常用的三角函数公式:
1. 正弦函数(Sine Function):$\sin\alpha=\frac{a}{c}$;
2. 余弦函数(Cosine Function):$\cos\alpha=\frac{b}{c}$;
3. 正切函数(Tangent Function):$\tan\alpha=\frac{a}{b}$。
其中,标识符号 $\sin$、$\cos$ 和 $\tan$ 分别代表正弦、余弦和正切函数。
由于我们已知其中一个角度 $\alpha$ 和与其相邻的一条边长 $a$,我们可以使用正弦函数或余弦函数来计算该三角形的斜边长 $c$。
若我们使用正弦函数,则有 $\frac{a}{c}=\sin\alpha$,整理得到 $c=\frac{a}{\sin\alpha}$。
若我们使用余弦函数,则有 $\frac{b}{c}=\cos\alpha$,整理得到 $c=\frac{b}{\cos\alpha}$。
综上,我们可以通过已知的角度与边长来计算直角三角形的斜边长。
