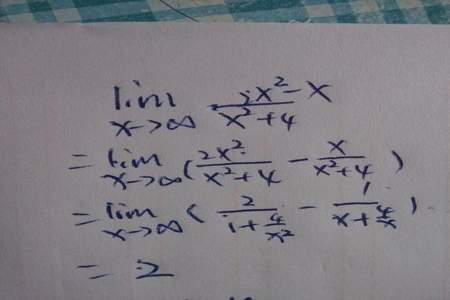
极限计算公式是用来计算函数在某一点或趋于某一点时的极限值的公式。以下是一些常用的极限计算公式:
1.基本极限:
lim(c) = c,其中c是常数。
lim(x) = x,其中x是自变量。
lim(a^x) = a^c,其中a是常数且a>0,c是常数。
lim(log_a(x)) = log_a(c),其中a是常数且a>0,c是常数。
求极限lim=
在高等数学中,极限是一个重要的概念.
极限可分为数列极限和函数极限,分别定义如下.
数列极限:
设为数列,A为定数.若对任给的正数ε,总存在正整数N,使得当n>N时,有
|An - A|<ε,
则称数列收敛于A,定数A称为数列的极限,并记作
lim An = A,或 An->A(n->∞),
读作“当n趋于无穷大时,An的极限等于A或An趋于A”.
函数极限:
设f为定义在[a,+∞)上的函数,A为定数.若对任给的ε>0,存在正数M(>=a),使得当x>M时有:
|f(x)-A|<ε,
则称函数f当x趋于+∞时以A为极限,记作
lim f(x) = A 或 f(x)->A(x->+∞)
