知道三角形的三条边长，如何求夹角

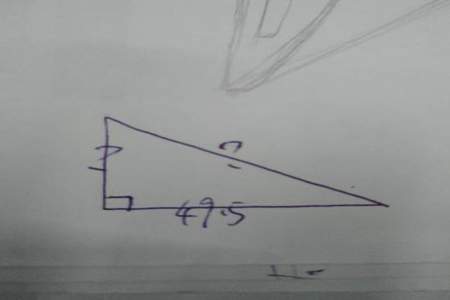
已知三角形的三条边长 a、b、c，可以使用余弦定理来求解夹角。余弦定理表达式如下：

cosA = (b² + c² - a²) / (2bc)

cosB = (a² + c² - b²) / (2ac)

cosC = (a² + b² - c²) / (2ab)

其中，A、B、C分别表示对应的三个夹角，a、b、c表示对应的三条边长。

使用以上公式，可以求出三个夹角的余弦值，然后通过反余弦函数（acos）可以得到对应的角度值。

需要注意的是，当给定的三条边长无法构成一个三角形时，无法使用余弦定理来求解夹角。

知道三角形的三条边长，如何求夹角

要计算一个三角形的夹角，你可以使用余弦定理。根据余弦定理，夹角的余弦值等于三角形两条边的平方和减去第三条边的平方，再除以两倍的两条边的乘积。具体计算公式如下：

cosθ = (a^2 + b^2 - c^2) / (2ab)

其中，a、b和c分别代表三角形的三条边长，θ代表夹角。

为了求得夹角θ，你可以将夹角的余弦值代入反余弦函数，即可得到夹角的弧度值。最后，将弧度值转化为度数，即可得到夹角的度数。

需要注意的是，夹角的度数通常是在0°到180°之间。如果夹角的度数大于180°，则需要通过减去360°的倍数来将其转化为0°到180°的范围内。同样地，如果夹角的度数小于0°，则需要通过加上360°的倍数来将其转化为0°到180°的范围内。

知道三角形的三条边长，如何求夹角

已知三角形的三条边a、b、c，三个角α、β、γ，可以由余弦定理得到三角形的三个内角。

cosA=（b平方+c平方-a平方）/2cb

cosB=（a平方+c平方-b平方）/2ac

cosC=（a平方+b平方-c平方）/2ab

余弦定理的含义是对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。

知道三角形的三条边长，如何求夹角

已知三角形边长，计算三角形的角度过程如下：

1、设三角形中角A所对应的边长是a，角B所对应的边长是b，角C所对应的边长是c。再利用公式：

①CosA=(c^2+b^2-a^2)/2bc

②CosB=(a^2+c^2-b^2)/2ac

③CosC=(a^2+b^2-c^2)/2ab

算出每一个角的余弦值，利用计算器上的反余弦函数功能就可以计算出各自的角度值。

2、如果三角形是钝角三角形，计算出的钝角的余弦值是负的，角度也就是负的，这时要加上180度才是钝角的角度。（注：a^2+b^2-c^2=0说明C的角度等于90度）