角平分线的性质定理

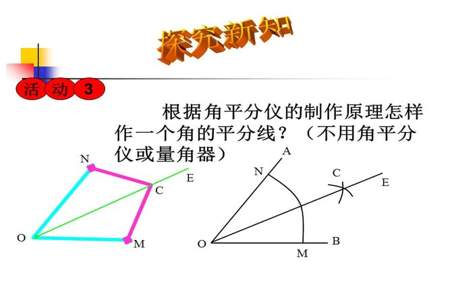
角平分线可以得到两个相等的角。

2.角平分线上的点到角两边的距离相等。

3.三角形的三条角平分线交于一点，称作三角形内心。三角形的内心到三角形三边的距离相等。

4.三角形一个角的平分线，这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例。

角平分线的性质定理

具体来说，对于一个角ABC，如果有一条线AD，使得∠BAD = ∠DAC，那么线AD就是角ABC的平分线。这意味着角ABC被平分成两个相等的角∠BAD和∠DAC。

角平分线的性质定理在几何学中有广泛的应用，可以用于证明角的相等、相似等性质，以及解决一些与角相关的问题。

角平分线的性质定理

一般角平分线的性质定理有两个：

1. 角平分线定理：如果一条直线将一个角分成两个相等的角，那么这条直线称为这个角的角平分线。

2. 角平分线定理的逆定理：如果一条直线是一个角的角平分线，那么它将这个角分成两个相等的角。

这两个定理表明，如果给定一个角ABC和一条它的内部直线AD作为它的一条角平分线，那么∠BAD = ∠DAC，并且反过来，在已知∠BAD = ∠DAC 的情况下，可以得出直线AD是∠BAC的一条角平分线。

利用这些性质可以解决很多相关问题，例如在已知三角形三边长度情况下求其内部某个角度大小等问题

角平分线的性质定理

角平分线的性质：

角平分线上的点到这个角的两边的距离相等.

这是角平分线学习的重点，涉及角平分线的题目大都会运用到这个性质。