当一条边的边长固定时，怎样可以得到周长最小的三角形

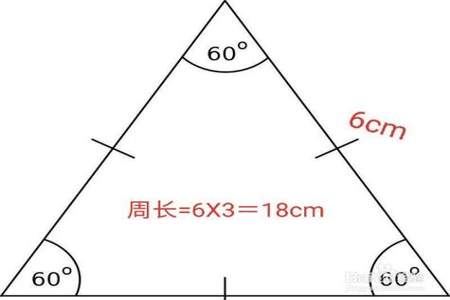
当一条边的边长固定时，要得到周长最小的三角形，需要使其他两条边尽可能接近这条边的长度。

根据三角形的性质，两条边之和必须大于第三条边的长度。因此，为了使周长最小，我们可以选择另外两条边的长度尽可能接近这条边的长度。具体来说，如果一条边的长度为a，我们可以选择另外两条边的长度都为a，这样可以得到一个等边三角形，周长最小。因为在等边三角形中，每条边的长度都相等，所以周长最小。

所以，当一条边的边长固定时，选择另外两条边与这条边等长，可以得到周长最小的三角形。

当一条边的边长固定时，怎样可以得到周长最小的三角形

    当固定边所对应的角越大，三角形周长越小。当这个角无限接近180度时，三角形周长最小。

    因为三角形两边之和大于第三边，当已固定边所对应的角无限接近180度时，另两边之和就无限接近这条边。所以，这时得到的三角形周长最小。

当一条边的边长固定时，怎样可以得到周长最小的三角形

1、将两个三角形重合，2、绕最长边中点，将一个三角形旋转180°，3、这时两个三角形组成的平行四边形周长最小。周长最小值=2×(三角形两小边之和)。