十字相乘法适用于哪些范围

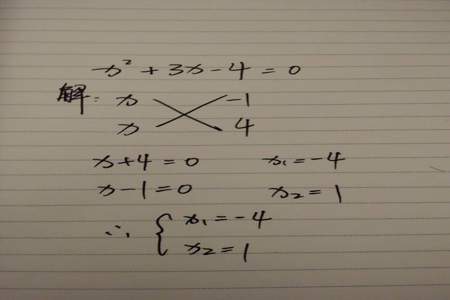
十字相乘法（Cross-multiplication）是一种求解二次方程的方法，它的适用范围主要局限于二次方程，尤其是一元二次方程。一元二次方程的一般形式为：

ax² + bx + c = 0

其中 a、b 和 c 是系数，x 是未知数。

对于这类方程，我们可以使用十字相乘法来求解。具体步骤如下：

1. 提取二次项系数 a，并将其与常数项 c 相乘，得到 ac。

2. 将二次项系数 a 与一次项系数 b 相乘，得到 ab。

3. 交叉相乘，即将 ac 乘以 b，并将 ab 乘以 c，然后将两个结果相加：ac × b + ab × c = acb + bca。

4. 将相加后的结果加上一次项系数 b 的平方：(ac × b + ab × c) + b²。

5. 开平方：√[(ac × b + ab × c) + b²]。

最终得到的结果是两个解，它们分别是：

x1 = (-b + √[(ac × b + ab × c) + b²]) / (2a)

x2 = (-b - √[(ac × b + ab × c) + b²]) / (2a)

需要注意的是，十字相乘法仅适用于一元二次方程。对于多元二次方程、高次方程以及其他类型的方程，这种方法并不适用。

十字相乘法适用于哪些范围

十字分解法的方法是：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数。

其实就是运用乘法公式(x+a)(x+b)=x²+(a+b)x+ab的逆运算来进行因式分解。

十字分解法能用于二次三项式（一元二次式）的分解因式（不一定是整数范围内）。

对于像ax²+bx+c=(a1x+c1）(a2x+c2）这样的整式来说，这个方法的关键是把二次项系数a分解成两个因数a1,a2的积，把常数项c分解成两个因数c1,c2的积，并使a1c2+a2c1正好等于一次项的系数b。

那么可以直接写成结果:ax²+bx+c=(a1x+c1）(a2x+c2）。

在运用这种方法分解因式时，要注意观察，尝试，并体会，它的实质是二项式乘法的逆过程。

当首项系数不是1时，往往需要多次试验，务必注意各项系数的符号。基本式子：x²+(p+q）x+pq=(x+p）(x+q）。

十字相乘法适用于哪些范围

十字相乘法可以用于两个整数相乘，并且两个整数都没有太多位数的情况下，适用范围比较广泛。通常情况下，两个整数的位数较少时，可以使用十字相乘法求积计算，当两个整数的位数过多时，使用十字相乘法计算的复杂度就会增加，建议使用其他高效的算法进行计算。一般来说，十字相乘法适用于两个整数的位数不超过三位数时比较合适。

十字相乘法适用于哪些范围

十字相乘法是因式分解中十四种方法之一，十字左边相乘等于二次项，右边相乘等于常数项，交叉相乘再相加等于一次项。十字相乘法适用范围：适用于二次三项式ax2+bx+c形式的。但并不是所有的二次三项式都可以。十字相乘法的技巧在于：不管常数项是多复杂,只要你能把它拆成两项m和n,然后试着用十字相乘法,试着将常数项分解成m*n的形式,然后使m+n等于一次项系数(需要去试着去凑)而且,当二次项的系数是1时才可以是m+n等于一次项常数，一般说能用十字相乘法做的,则一定可以拆成功的。

十字相乘法适用于哪些范围

十字相乘法是一种用于计算两个数的乘积的简便方法，适用于任何范围的数。无论是小数、分数、整数还是大数，十字相乘法都可以使用。它是一种基本的乘法计算方法，可以在手算时快速计算乘积。无论是小学生学习乘法，还是在日常生活或工作中需要进行乘法计算，十字相乘法都是一种常用的计算方法。