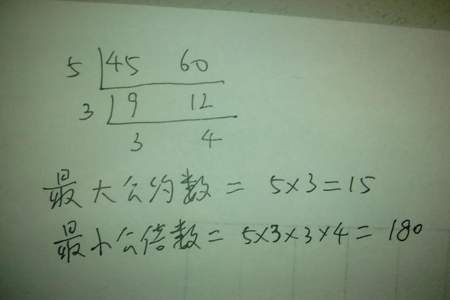
有多种方法可以求最大公因数,以下是其中两种常用的方法:
1.辗转相除法:假设要求两个数a和b的最大公因数,首先将较大的数除以较小的数,得到余数c1,然后将较小的数除以余数c1,得到余数c2,依次类推,直到余数为0,此时除数即为最大公因数。
2.质因数分解法:将两个数分别分解质因数,然后将它们的公共因数相乘,得到的积即为最大公因数。
例如,求出24和36的最大公因数:
1.辗转相除法:36 ÷ 24 = 1 余12,24 ÷ 12 = 2 余0,因此最大公因数为12。
2.质因数分解法:24 = 2 × 2 × 2 × 3,36 = 2 × 2 × 3 × 3,它们的公共因数为2 × 2 × 3 = 12,因此最大公因数为12。
怎样求最大公因数
最大公因数可以通过以下方法求得:先列出两个数的所有因数,然后找出它们共有的因数,再从中选取最大的那个因数即为最大公因数。
例如,求30和45的最大公因数:30的因数为1、2、3、5、10、15、30,45的因数为1、3、5、9、15、45,它们共有的因数为1、3、5、15,其中最大的因数为15,因此,30和45的最大公因数是15。
同时,这个方法也适用于多个数的最大公因数的求解。
怎样求最大公因数
1、分解质因数法
分解质因数:每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数。
求12和8的最大公因数
12=2×2×3: 8=2×2×2
所以12和8的最大公因数是2×2=4
2、短除法。
短除符号就是除号倒过来,在除法中写除数的地方写两个数共有的质因数,然后写下两个数被公有质因数整除的商,之后再除,以此类推,直到结果互质为止。
如: 求12和8的最大公因数
2 12 8
2 6 4
3 2
所以12和8的最大公因数是2×2=4
怎样求最大公因数
求最大公因数的方法:
方法一:质因数分解法
质因数分解法是求最大公因数的一种常用方法。它的基本思想是将两个数分别分解成质因数的乘积,然后找出它们的公共质因数,最后将这些公共质因数相乘即可得到最大公因数。
方法二:辗转相除法
辗转相除法是求最大公因数的另一种常用方法。它的基本思想是用较大的数除以较小的数,然后用余数去除较小的数,直到余数为0为止,此时较小的数就是最大公因数。
方法三:欧几里得算法
欧几里得算法是求最大公因数的一种高效方法。它的基本思想是用较大的数除以较小的数,然后用余数去除较小的数,直到余数为0为止,此时较小的数就是最大公因数。
方法四:连续整数检验法
连续整数检验法是求最大公因数的一种简单方法。它的基本思想是从1开始,依次检验两个数能否被这个数整除,直到找到最大公因数为止。
怎样求最大公因数
几个数的公因数中最大的一个公因数叫做这几个数的最大公因数。求最大公因数常用的有列举法、分解质因数法、辗转相除法和短除法等。其中,辗转相除法和短除法是比较快速和高效的方法。
辗转相除法是将两个数字中的数值较大者作为被除数,另一个作为除数的值,然后将被除数除以除数,得到一个余数,将上一步骤得到的余数作为新的被除数,再用除数去除该被除数。
怎样求最大公因数
1.写因数。先写出各自的因数,再找到公有的因数,再找到最大公因数。这是新版本中最基础的方法。用图形。先写出公有的因数,再分别写出各自的因数。分解质因数。先分别分解质因数,再找到公有的质因数,如果是两个以上就要把公有的质因数相乘,积就是最大公因数;如果只有一个,那这个质因数就是几个数的最大公因数。
2.断除法。利用断除法求几个数的最大公因数。先写数字,然后用它们的质因数做除数,直到商为互质数为止。(左边的2、2、3就是除数,下面的2.、3就是商)如果除数是一个,那这个就是几个数的最大公因数,如果除数是两个以上,那除数相乘的积就是几个数的最大公因数。
