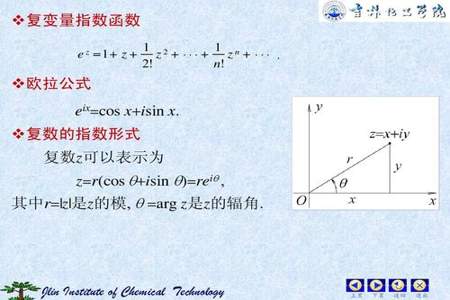
设z=a+bi((a、b∈R)),那么tanθ=b/a,θ为幅角。
1、复数的辐角在复变函数中,自变量z可以写成z=r*cosθ+isinθ。将复数的实部与虚部的平方和的正的平方根的值称为该复数的模,记作∣z∣,即对于复数z=a+bi,它的模∣z∣=√a^2+b^2复数的集合用c表示,实数的集合用r表示。
2、r是z的模,即r=|z|,θ是z的辐角,记作argz。辐角是复数中的概念,所有复数都可以表示为cosa+isina的形式,其中a(0=<a<360度)就是辐角;极坐标中是极角,那根表示出来的向量里,长度就是模,辐角就是与实轴的夹角。
3、在-π,π间的辐角称为辐角主值,记作argz。z=ρe^iφ为该复数的指数式,其中ρ为该复数的模,φ称为该复数中的辐角,记作Argz,一个复数的辐角值不能唯一地确定,可以取无穷多个值,并且彼此相差2π的整数倍。
复数的辐角主值的概念
概念是指任意一个不为零的复数z=a+bi的辐角有无限多个值,且这些值相差2π的整数倍。把适合于0<θ≤2π的辐角θ的值,叫做辐角的主值,记作arg(z)1。
复数的辐角主值的概念
中文名 辐角主值
外文名 principal argument angle
别 称 主辐角
区 间 (-π,π]
定义
复数的模与辐角是复数三角形式表示的两个基本元素,复数所对应的向量长度称为复数的幅值,该向量与实轴正方向的夹角为复数的辐角。辐角的大小有无穷多,但是辐角主值唯一确定。
复数的辐角主值的概念
在复平面上,复数所对应的向量与x轴正方向的夹角称为复数的辐角,显然一个复数的辐角有无穷多个,但是在区间(0,2π]内的只有一个,这个辐角就是该向量的辐角主值,也称主辐角,记为argz。
