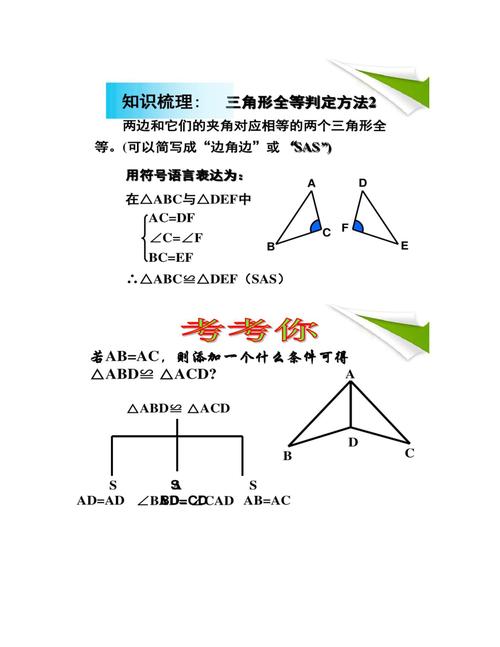
三角形全等的三个判定定理是
边边边定理(SSS),
边角边定理(SAS),
角角边定理(AAS)
证明如下
已知三角形△ADC与三角形ACB中,∠D=90
°,∠C=90°,且满足AD=CB, BD=CA,可以推出△ADB≌△ACB(边角边SAS),如果设DB与CA交于O,如果三角形△ADO与三角形△OCB为等腰三角形,则会有AD=BC,AO=BO,DO=CO,则△ADO≌△OCB(边边边SSS).由上面可知,既然△ADO与△OCB为等腰三角形,那么∠D与∠C一定相同,那么存在∠DAO=△COB,AD=CB,∠ADO=∠COB故有△ADO
≌△COB(角边角ASA)
asa全等三角形定理推导
ASA全等三角形定理是指:若两个三角形的某个角度相等,另外两个角度和对应边分别相等,则这两个三角形全等。
下面是ASA全等三角形定理的推导过程:
假设有两个三角形ABC和DEF,满足下列条件:
- ∠A = ∠D (条件1,即两个三角形的某个角度相等)
- AB = DE (条件2,即对应边相等)
- ∠B = ∠E (条件3,即另外两个角度相等)
- AC = DF (条件4,即对应边相等)
我们需要证明,根据这四个条件,可以得出三角形ABC和三角形DEF全等。
证明:
由条件1可知,∠A = ∠D,因此可以做出一条从点B到DE的线段BD,并使∠ABD = ∠DED。此时,三角形ABD和三角形DEB具有以下相等的部分:
- ∠ABD = ∠DEB (因为∠ABD = ∠DED)
- AB = DE (已知条件2)
因此,根据相等的对应关系,可以得出AD = DB,BE = ED。
接下来,比较三角形ACD和三角形DFE。由条件1和条件3可知,这两个三角形的两个角度相等:
- ∠ACD = ∠DFE (因为∠A = ∠D和∠B = ∠E)
由条件4可知,这两个三角形的一条边相等:
- AC = DF
由以上证明可知,三角形ABD和三角形DEB相等,而且AD = DB和BE = ED。将它们放在一起,可以得到以下关系:
- AD + BE = DB + ED
- AC = DF
根据公理1和公理2,可以得到以下关系:
- AB + BC = DE + EF
- AC = DF
因此,三角形ABC和三角形DEF全等。
asa全等三角形定理推导
SSS,SAS,ASA,AAS,HL 也就是 1、三组对应边分别相等的两个三角形全等(简称SSS)。
2、有两边及其夹角对应相等的两个三角形全等(SAS)。
3、有两角及其夹边对应相等的两个三角形全等(ASA) 注:S是边的英文缩写,A是角的英文缩写 由3可推到 4、有两角及一角的对边对应相等的两个三角形全等(AAS) 5、直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(HL)
