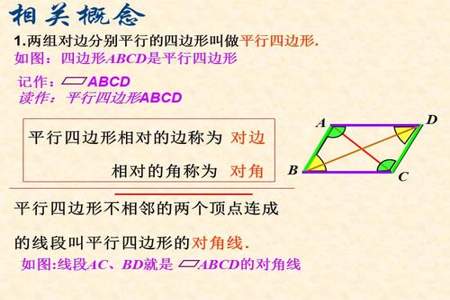
平行四边形的定理是指,如果一个四边形的对边是平行的,则该四边形是平行四边形,并且具有以下特征:
对边相等:平行四边形的对边长度相等,即两边两边地对应相等。
对角线互相平分:平行四边形的对角线互相平分,即将对角线分成相等的两部分。
内角和为180度:平行四边形的内角和为180度,也就是说,四个内角的和等于180度。
这些特征是平行四边形独有的,通过检查对边是否平行可以确定一个四边形是否为平行四边形。同时,在解决平行四边形相关的几何问题时,可以使用这些特征来推导和证明结论。
平行四边形的定理是什么
首先给出答案:在同一个二维平面内,由两组平行线段组成的闭合图形,称为平行四边形,其边与边、角与角、对角线之间存在着各种各样的关系,即是平行四边形性质定理。
定义:
有两组对边分别平行的四边形叫做平行四边形,包括长方形、菱形、正方形和一般平行四边形,其边与边、角与角、对角线之间存在着各种各样的关系,即是平行四边形性质定理。
性质
两组对边平行且相等;
两组对角大小相等;
相邻的两个角互补;
对角线互相平分;
对于平面上任何一点,都存在一条能将平行四边形平分为两个面积相等图形、并穿过该点的线;
四边边长的平方和等于两条对角线的平方和[1]。
分类
矩形、菱形、正方形是特殊的平行四边形。
判定定理:
(1)定义法:两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)两组对角分别相等的四边形是平行四边形;
(4)对角线互相平分的四边形是平行四边形;
(5)一组对边平行且相等的四边形是平行四边形。
