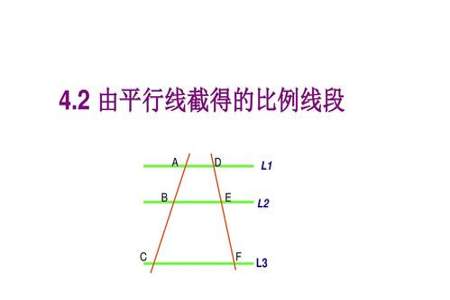
如果三条线段两两平行,则它们所在的直线也两两平行。这是平行线的传递性质,也是欧氏几何中的基本定理之一。具体来说,如果线段AB、CD、EF两两平行,则它们所在的直线AB、CD、EF也两两平行。这个定理在几何学中有着广泛的应用,例如在平面几何中,可以用来证明平行四边形的性质,以及在空间几何中,可以用来证明平面与平面的关系等。
三条线段平行可得什么性质
两直线都与第三条直线平行,那么这两条直线也互相平行。(若直线a平行于直线b,直线b平行于直线c,那么直线a也平行于直线c)(等量代换)。
三条线段平行可得什么性质
在同一平面内,不相交的两条直线叫做平行线。平行线的性质:
(1)两条平行线被第三条直线所截,同位角相等;
(2)两条平行线被第三条直线所截,内错角相等;
(3)两条平行线被第三条直线所截,同旁内角互补。平行线的判定定理:
(1)两条直线被第三条直线所截,如果同位角盯单驰竿佻放宠虱触僵相等,那么这两条直线平行;
(2)两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行;
(3)两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线平行。
三条线段平行可得什么性质
可以得到三条线段中任意两条线段相互平行
