要证明两个等腰三角形的底边平行,可以使用以下方法之一:
1. 使用等腰三角形的性质。
如果两个三角形都是等腰三角形,它们的两条边和顶角都相等。如果能证明两个等腰三角形的顶角相等,那么它们的底边就是平行的。
可以通过比较等腰三角形的边长和顶角大小来进行推导,并使用角度和边的对应关系来得出结论。
2. 使用平行线的性质。
如果能证明两个等腰三角形的底边上的某两个对应点分别位于平行的直线上,那么可根据平行线的性质得出结论,即底边平行。
可以通过使用平行线的定义或平行线的判定方法,如同位角相等、内错角相等等来进行推导。
无论使用哪种方法,推导过程都需要仔细、逻辑性强。需要根据具体的等腰三角形和相关条件进行推理和论证。
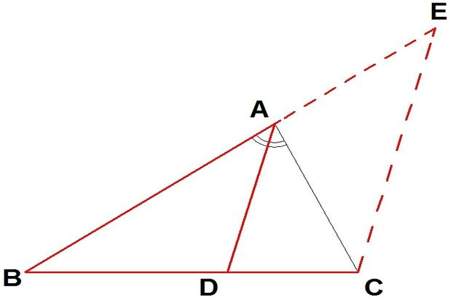
怎么证明两个等腰三角形底边平行
设AC=x,BC=y
DC=x-0.618x=0.382x
EC=y-0.618y=0.382y
DC/EC=0.382x/0.382y=x/y
DC/EC=AC/BC
因为角C=角C
所以两个三角形CDE与CAB相似
DE/AB=DC/AC
