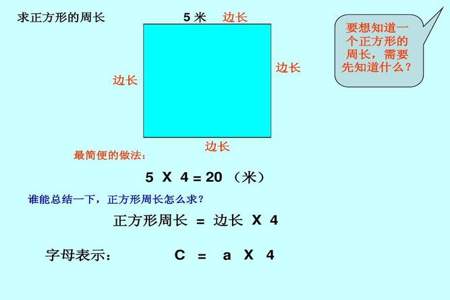
正方形的周长大.
设正方形的边长为 a .圆的半径为 r .
则正方形的周长为 4a .圆的周长为 2πr .
因为,a² = πr²
a = √π × r
则有,4a = 4√π × r = 2×2√π × r > 2πr .
所以,面积相等时,正方形的周长比圆的周长大.
面积相同的圆和正方形,哪个周长大
圆和正方形的面积相同时,圆的周长一定比正方形的周长更大。这是因为,圆的面积是由 $\pi$ 和半径的平方相乘得到的,而周长是由 $\pi$ 和半径相乘得到的。因此,当面积相同时,圆的半径相对于正方形的边长要更短,但圆的周长却由于 $\pi$ 的存在而变得更大。另一方面,正方形的周长只是由其边长相乘得到的,因此相对于圆来说边长更长,但周长更短。因此,当面积相同时,圆的周长会更大。
