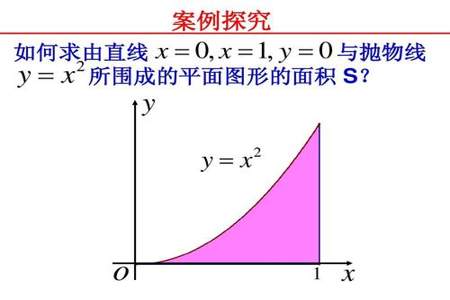
要求抛物线与直线围成图形的面积,可以使用积分方法。首先,你需要找到抛物线和直线的交点,这些交点将确定积分的上下限。
假设你有一个抛物线方程 f(x) 和一条直线方程 g(x)。首先,找到它们的交点,解方程 f(x) = g(x),以找到 x 值。这些 x 值将成为积分的上下限。
接下来,你可以使用定积分来计算图形的面积。在这种情况下,你将计算两个函数之间的面积差:
1. 找到交点后,设置定积分的上下限为这些 x 值。
2. 计算被抛物线和直线所夹区域的面积,使用积分表达式:
面积 = ∫[a, b] |f(x) - g(x)| dx
其中,[a, b] 是交点的 x 范围,|f(x) - g(x)| 表示两个函数之间的绝对值。
3. 计算这个定积分,得到图形的面积。
请注意,如果抛物线和直线交叉多次,你可能需要分割积分范围,并分别计算每个区域的面积,然后将它们相加,以获得整体图形的面积。
