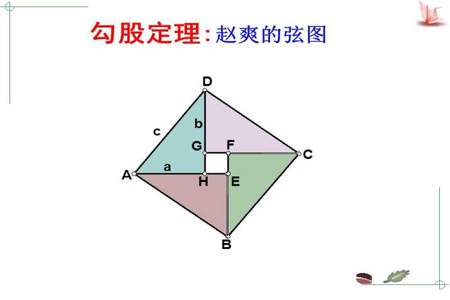
勾股定理的验证方法有很多种,以下是其中一些常用的方法:
1. 直接证明:这是最直接的证明方法,通过构造直角三角形,利用勾股定理的定义直接证明。
2. 辅助图形证明:利用平行四边形、矩形、正方形等辅助图形,通过证明这些图形的面积或周长与直角三角形的面积或周长之间的关系,从而证明勾股定理。
3. 相似三角形证明:利用相似三角形的性质,证明直角三角形的边长比例与斜边长度比例相等,从而证明勾股定理。
4. 切比雪夫不等式证明:利用切比雪夫不等式,证明直角三角形的边长满足勾股定理。
5. 利用向量证明:通过向量的内积、模长等概念,证明勾股定理。
6. 利用三角函数证明:利用正弦、余弦、正切等三角函数的性质,证明勾股定理。
7. 利用概率论证明:通过概率论的方法,证明在一定条件下,直角三角形的边长满足勾股定理。以上只是勾股定理的部分验证方法,实际上还有许多其他证明方法。每种方法都有其特点和优势,适用于不同的问题和场景。
