全等三角形是指两个三角形在形状和大小上完全相等。判定两个三角形全等的方法主要有两种:边边边(SSS)和三边对应相等(SAS)。以下是全等三角形的判定公式:
1. 边边边(SSS):如果两个三角形的三边分别相等,那么这两个三角形全等。
- a = a'(第一条边的长度相等)
- b = b'(第二条边的长度相等)
- c = c'(第三条边的长度相等)
2. 三边对应相等(SAS):如果两个三角形有两边及其夹角分别相等,那么这两个三角形全等。
- a = a'(第一条边的长度相等)
- |α = α'|(两个对应角相等)
- b = b'(第二条边的长度相等)
请注意,这里使用的符号 |α = α'| 表示两个角相等。在实际应用时,我们通常不需要显式地表示角度相等,因为角的大小是根据边长的比例来确定的。当两边及其夹角分别相等时,我们可以推断这两个三角形是全等的。
除了以上两种方法,还有边角边(SAS)、角边角(ASA)和角角边(AAA)等其他判定全等三角形的方法。在实际问题中,需要根据已知条件灵活选择合适的判定方法。
数学的全等三角形公式
S.A.S. (Side-Angle-Side)(边、角、边):各三角形的其中两条边的长度都对应地相等,且两条边夹着的角都对应地相等的话,该两个三角形就是全等。A.S.A. (Angle-Side-Angle)(角、边、角):各三角形的其中两个角都对应地相等,且两个角夹着的边都对应地相等的话,该两个三角形就是全等。
数学的全等三角形公式
数学中有一组全等三角形的公式,包括以下几种:
1. SSS(边-边-边):如果两个三角形的三条边分别对应相等,则这两个三角形全等。
2. SAS(边-角-边):如果两个三角形的两条边和夹角对应相等,则这两个三角形全等。
3. ASA(角-边-角):如果两个三角形的两个夹角和夹边对应相等,则这两个三角形全等。
4. AAS(角-角-边):如果两个三角形的两个夹角和非夹边对应相等,则这两个三角形全等。
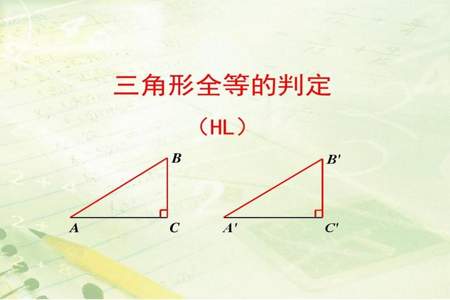
5. RHS(直角边-斜边-直角边):如果两个直角三角形的斜边和一个直角边对应相等,则这两个三角形全等。
这些全等三角形公式可以用来判断两个三角形是否全等。
