全等三角形性质和定义的区别

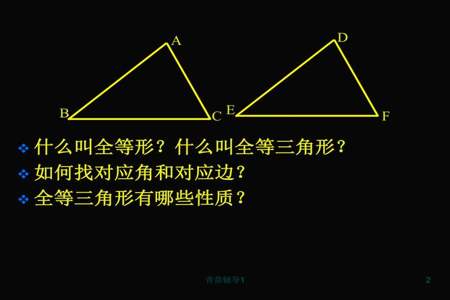
区别是：全等三角形的定义，既可作为判定两个三角形全等的方法，也可作为全等三角形的性质，而全等三角形的性质仅是性质，不能作为全等的判定方法。

全等三角形性质和定义的区别

区别在性质是由图形得规律，定义是由规律得到图形。定义：两个能完全重合的三角形是全等三角形。性质是：全等三角形的对应角相等，对应边相等。对应角平分线，高，中线都分别相等。

全等三角形性质和定义的区别

这是几何学中的重要概念之一，它描述了两个三角形的形状和大小完全相同的情形。全等三角形的性质和定义是相关联的，但也有所区别。

首先，让我们来介绍全等三角形的性质。全等三角形的性质是相对于其完全相同的特性而言的，也就是说，如果两个三角形全等，那么它们一定具有以下性质：

1. 对应边相等：全等三角形的对应边长相等。

2. 对应角相等：全等三角形的对应角度相等。

3. 对应中线相等：全等三角形的对应中线长度相等。

4. 对应高线相等：全等三角形的对应高线长度相等。

5. 对应角平分线相等：全等三角形的对应角平分线长度相等。

这些性质是全等三角形的本质特征，也是我们在解题和证明时经常使用的定理。

接下来，我们来介绍全等三角形的定义。全等三角形的定义是指，如果一个三角形的三条边长和三个角度都与另一个三角形完全相同，那么这两个三角形就被认为是全等的。这个定义可以从两个方面来理解：

1. 对应边相等：全等三角形的对应边长必须相等。

2. 对应角相等：全等三角形的对应角度必须相等。

需要注意的是，全等三角形的定义不仅包含了性质，而且还对其进行了严格的限制。只有当两个三角形的所有边长和角度都完全相同时，它们才能被视为全等三角形。因此，我们在解题和证明时，需要严格遵循这个定义，以确保我们的结论是正确的。

全等三角形的性质和定义是相关的，但也有所区别。性质是全等三角形的固有特征，而定义则是对其进行了严格的限制。只有当我们正确理解并掌握了全等三角形的性质和定义，才能在几何学中更好地运用它们解决问题。

全等三角形性质和定义的区别

首先说他们的共同点都能判定两个三角形全等。再说区别定义要用到六对条件，三角，三边都要相对应相等才是全等。而判定定理只用到三三对条件两边一角或两角，一边或三边对应相等，就可以判断两个三角形全等了。也就是性质判断全等相对要简单一些。

全等三角形性质和定义的区别

全等三角形的性质是指两个三角形在大小和形状上完全相同。当两个三角形的对应的角度相等，并且对应的边长也相等时，它们就是全等三角形。全等三角形的性质包括：

1. 恒等对应定理：如果两个三角形的三个角分别相等，则它们是全等的。

2. SSS（边-边-边）判定条件：如果两个三角形的三条边对应相等，则它们是全等的。

3. SAS（边-角-边）判定条件：如果两个三角形的两条边和夹角对应相等，则它们是全等的。

4. ASA（角-边-角）判定条件：如果两个三角形的两个角和夹边对应相等，则它们是全等的。

而全等三角形的定义是指具有相同大小和形状的两个三角形。也就是说，当两个三角形的对应的角度相等，并且对应的边长也相等时，我们可以称它们为全等三角形。全等三角形的定义与性质是相辅相成的，性质用于判定两个三角形是否相等，而定义则用于描述两个三角形是否具有相等的角和边长。

全等三角形性质和定义的区别

全等三角形是指具有对应边相等且对应角也相等的两个三角形。

性质是指描述两个三角形之间关系的一些规则或特点，例如全等三角形具有稳定性，即经过旋转或翻转后能够与自身重合。

全等三角形的定义是指具有对应边相角也相等的两个三角形完全重合。也就是说，两个三角形必须满足所有对应边相等且对应角相等的条件才能被称为全等三角形。

因此，全等三角形性质和定义的区别在于前者是描述两个三角形之间的关系，而后者是描述两个三角形完全重合的条件。