三角形两边之差等于第三边的情况

在一个三角形中，两边之差等于第三边的情况是不可能的。

根据三角形的性质，对于任意三边长度为 a、b 和 c 的三角形，以下两个条件必须同时满足：

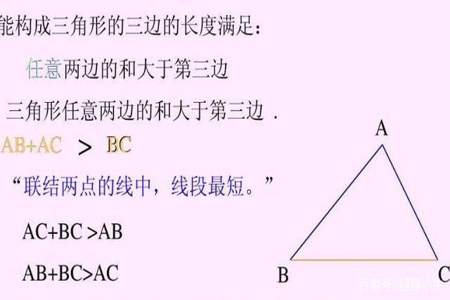
任意两边之和必须大于第三边：a + b > c，a + c > b，b + c > a。这是三角形的三角不等式定理。

任意两边之差必须小于第三边：|a - b| < c，|a - c| < b，|b - c| < a。

如果两边之差等于第三边，则违反了三角形的性质，无法构成一个有效的三角形。

三角形两边之差等于第三边的情况

这是四年级上册学的知识点，任何一个三角形，任意两边的和大于第三边，任意两边的差小于第三边，三角形两边之差，如果等于第三边，它就构不成一个三 角形。例如，三边分别是三厘米，四厘米，五厘米，可以构成一个三角形。一厘米，二厘米，三厘米，构不成一个三角形。

三角形两边之差等于第三边的情况

        题目中的三角形两边之差不可能等于第三边。

        三角形的基本原理告诉我们，任何三角形的任意两边之和一定大于第三边。假设三角形ABC，那么三条边分别就是AB、BC、CA，长度为分别是a、b、c。根据上述基本原理，a+b＞c，b+c＞a，c+a＞b。如果题目中给出的假设成立，即两边之差等于第三边，则假设a-b=c，将该式代入前面第二式，就会变成b+c=b+（a-b）=a＞a，显然这是错误的，这就反正了题目中给出的假设的错误性。

三角形两边之差等于第三边的情况

在一个三角形中，两边之差必须小于第三边的长度，否则无法构成一个有效的三角形。

具体来说，如果我们把三角形的三条边长度分别表示为a、b和c，那么必须满足以下条件之一：

1. a+b>c

2. a+c>b

3. b+c>a

如果以上三个条件中的任何一个不成立，那么这三条边就不能组成一个三角形。

举个例子，如果有一条边的长度是5，另一条边的长度是3，那么它们的差是2。根据以上条件，第三条边的长度必须大于2才能构成一个合法的三角形。