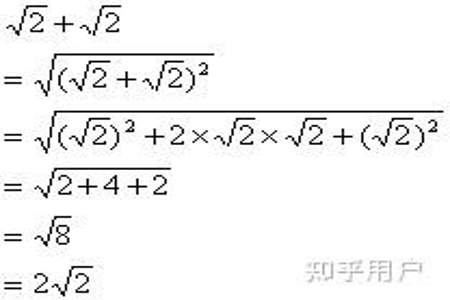
直角坐标系下,ds=(dx)2+(dy)2−−−−−−−−−−−√
这个是非常自然的一种微元角度。
通常给定的积分曲线是可以化为:y=y(x)型的
因此ds=1+(dydx−−−−−−√)2dx
等同于把dx提出来了
dydx=y′(x)
所以积分可以化为:
∫Lf(x,y)=∫baf(x,y(x))1+y′(x)2−−−−−−−−√dx
这是直角坐标系下的第一种。
ds为什么等于根号1+dx2+dy2
因为ds是由f(x)、f(y)组成的复合函数的积分。
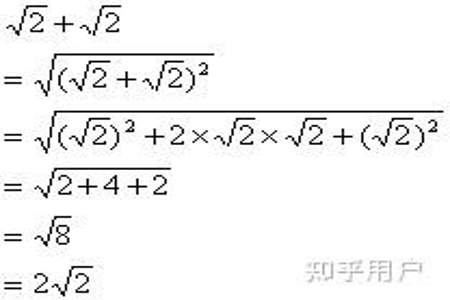
直角坐标系下,ds=(dx)2+(dy)2−−−−−−−−−−−√
这个是非常自然的一种微元角度。
通常给定的积分曲线是可以化为:y=y(x)型的
因此ds=1+(dydx−−−−−−√)2dx
等同于把dx提出来了
dydx=y′(x)
所以积分可以化为:
∫Lf(x,y)=∫baf(x,y(x))1+y′(x)2−−−−−−−−√dx
这是直角坐标系下的第一种。
ds为什么等于根号1+dx2+dy2
因为ds是由f(x)、f(y)组成的复合函数的积分。