100以内的奇数和偶数之和各是多少

100以内的奇数和偶数之和是5050。

100以内的奇数和为:1+3+5+…+99＝（1+99）×50÷2＝2500。

100以内的偶数和为:2+4+6+…+100＝（2+100）×50÷2＝2550。

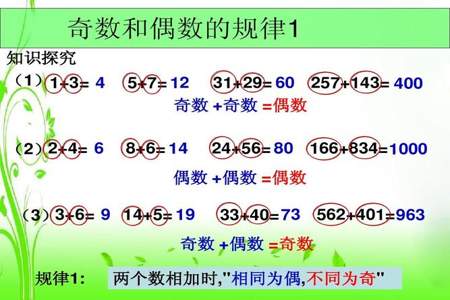
自然数（整数）可以分成奇数和偶数两大类。能被2整除的数叫做偶数，不能被2整除的数叫做奇数。

100以内的奇数和偶数之和各是多少

100以内的奇数和是：2500；100以内的偶数和是2550。

根据题意，我们可以得知题目要求我们对100以内的奇数数列和偶数数列进行求和。根据奇数和偶数的定义，我们可以得知：

100以内的奇数数列为：1+3+5...+99；

100以内所有偶数数列为：0+2+4+6+...+100。

根据等差数列求项数公式（项数＝（末项-首项）÷公差＋1），我们可以得知：

奇数数列项数为：(99−1)÷2+1=98÷2+1=49+1=50；

偶数数列项数为：(100−0)÷2+1=100÷2+1=50+1=51。

根据等差数列求和公式（和＝（首项＋末项）×项数÷2），我们可以得知：

100以内所有的奇数和为:

1+3+5...+99

=(1+99)×50÷2

=100×50÷2

=5000÷2

=2500

100以内所有偶数和为：

0+2+4+6+...+100

=(0+100)×51÷2

=100×51÷2

=5100÷2

=2550。