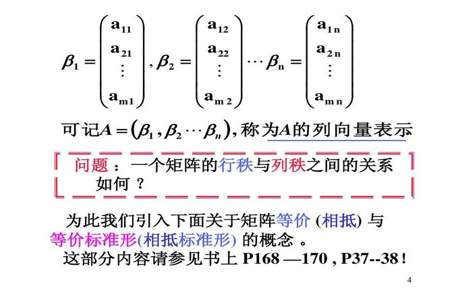
矩阵与其转置矩阵乘积的秩与矩阵的秩是相等的。具体来说,如果我们设A是一个m×n的矩阵,那么有r(A'A)=r(A)。其中,'表示转置操作。
这个结论可以通过以下方式进行证明:
1. 首先,我们可以观察到A'A是一个对称矩阵。
2. 然后,我们考虑两个n元齐次方程Ax=0和A'Ax=0。若Ax=0有非零解,那么将其代入A'Ax=0会得到A'Ax=0也有非零解。这表明两个方程同解。
3. 进一步,由于A'A是对称的,我们有R(A'A)=C(A'A)。而C(A'A)代表了其所有列向量的线性组合构成的空间,因此有r(A')+r(A')≥n,即r(A')≥n/2。同理,r(A)≥n/2。由于r(A')≤min{m,n}且r(A)≤min{m,n},我们有r(A')≤min\{m,n}且r(A)≤min\{m,n\}。因此,我们有r(A')+r(A')≥n,即r(A')≥n/2。同理,r(A)≥n/2。由于r(A')≤min\{m,n\}且r(A)≤min{m,n\},我们有r(A')≤min\{m,n\}且r(A)≤min\{m,n\}。因此,我们有r(A')+r(A')≥n,即r(A')≥n/2。同理,r(A)≥n/2。由于r(A')≤min\{m,n\}且r(A)≤min\{m,n\},我们有r(A')≤min\{m,n\}且r(A)≤min\{m,n}。因此,我们有r(A')+r(A')≥n,即r(A')≥n/2。同理,r(A)≥n/2。
由于r(A')≤min\{m,n\}且r(A)≤min\{m,n\},我们有r(A')≤min\{m,n}且r(A)≤min\{m,n\}。因此,我们有r(A')+r(AA)=n,即r(AA)= r(AA)。
矩阵与其转置矩阵乘积的秩与本身的秩
Ax=0自然有A*Ax=0,而A*Ax=0意味着(x,A*Ax)=0即(Ax,Ax)=0即Ax=0。所以A与A*A核空间相同,所以秩相等。
