立体图形是三维的物体,具有长度、宽度和高度。它们在数学和几何学中有广泛的应用,用于计算体积、表面积和其他属性。立体图形的面积和特点取决于其类型,以下是一些常见立体图形的面积和特点:
1. **立方体**:
- 面积:立方体有六个相等的正方形面,因此表面积等于六个面的面积之和。
- 特点:所有角都是直角,所有边长相等。
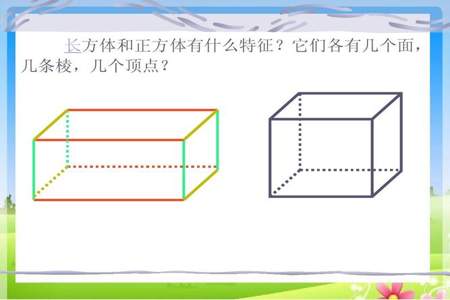
2. **长方体**:
- 面积:长方体有六个矩形面,可通过计算各个面的面积之和来得到表面积。
- 特点:与立方体不同,长方体的对角线可能不相等。
3. **圆柱体**:
- 面积:圆柱体有两个圆形底面和一个侧面,可以通过计算底面积和侧面积之和来得到表面积。
- 特点:侧面是一个矩形,两个底面是圆形。
4. **球体**:
- 面积:球体的表面积可以通过公式计算:\(4\pi r^2\),其中 \(r\) 为球的半径。
- 特点:球体没有边和顶点,表面是连续的。
5. **锥体**:
- 面积:锥体有一个圆形底面和一个侧面,可以通过计算底面积和侧面积之和来得到表面积。
- 特点:锥体的侧面是一个三角形,底面是一个圆形。
6. **棱锥**:
- 面积:棱锥的表面积取决于其底面形状和侧面形状,通常通过计算各个面的面积之和来得到表面积。
- 特点:棱锥的底面可以是任何多边形,侧面是三角形。
这些是一些常见的立体图形的面积和特点。要计算特定立体图形的表面积,需要了解其几何属性,包括各个面的形状和尺寸。不同类型的立体图形具有不同的特点和计算方法,因此在具体计算时需要考虑这些因素。
