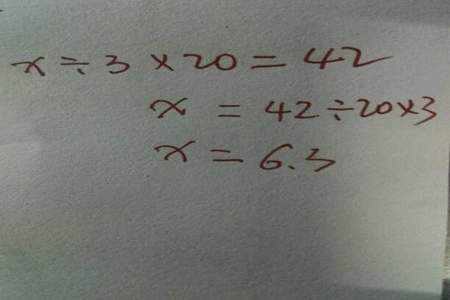
解小数点方程式的方法与解整数方程式类似,只需注意小数点的位置即可。下面是一些常见的解小数点方程式的方法:
1. 清除小数点:如果方程式中有小数点,可以通过乘以适当的倍数来将方程式转化为整数方程式。例如,如果方程式中有一个小数位,则可以乘以10,如果有两个小数位,则可以乘以100,以此类推。
2. 移项和合并项:将方程式中的项进行移项和合并项的操作,将未知数放在一边,已知数放在另一边,使方程式变为形如 "未知数 = 已知数" 的形式。
3. 解方程:根据方程式的形式,使用代数运算求解未知数。可以使用加减法、乘除法等基本运算来解方程。
4. 检查答案:将求得的未知数代入原方程式中,验证方程式的左右两边是否相等。如果相等,则所求解为正确答案;如果不相等,则需要重新检查计算过程。
请注意,在解小数点方程式时,要特别注意小数点的位置,确保计算过程中不发生错误。如果方程式较复杂或存在其他特殊情况,可能需要更高级的数学方法来解决。
小数解方程
解方程时,我们通常遇到整式方程、分式方程和根式方程。而小数解方程这个说法并不常见。我猜你可能是想了解如何处理带有小数的方程。
在处理带有小数的方程时,通常需要进行适当的代数变形,将小数系数移到等式另一边,从而消除小数。以下是一个简单的示例:
示例:解方程 2x - 0.5 = 3.2
解:首先,将常数项移到等式左边,未知数移到等式右边。
2x = 3.2 + 0.5
2x = 3.7
然后,将小数系数化简为整数。这里,我们将小数0.5扩大10倍,变为整数5。
2x = 3.7 * 10
2x = 37
最后,通过除法将未知数的系数化为1。
x = 37 / 2
x = 18.5
所以,这个带有小数的方程的解是 x = 18.5。
当然,实际遇到的方程可能会更复杂,需要运用更多的代数技巧和方法。但是,基本原理都是通过适当的代数变形,将方程化简为更易求解的形式。
