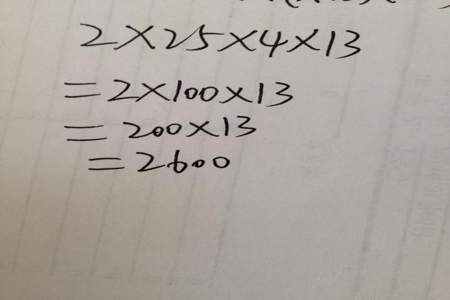
根据乘法运算的定义以及性质规定,上式可以使用乘法结合律和平方差公式进行简便运算,原式等于99×(101×99+1)=999×{(100+1)(100-1)+1}=999×(10000-1+1)=9990000。
用简便方法计算: 101x99x999+999
答:101x99Ⅹ999十999没有简便方法计算。这是一道乘法与加法的混合计算题,按照惯例,先乘后加。即:101Ⅹ99x999的积加999。
用简便方法计算: 101x99x999+999
101x99x999+999
=((100+1)*99+1)*999
=(100*99+99+1)*999
=10000*999
=9990000
101×99×999+999
=(101x99+1)x999
=[(100+1)(100-1)+1]x999
=(100x100-1x1+1)x999
=(10000-1+1)x999
=10000x999
=999000
扩展资料
简便运算:
1、运用乘法的交换律、结合律进行简算。
如:2.5×0.125×8×4等,如果遇到除法同样适用,或将除法变为乘法来计算。如:8.3×67÷8.3÷6.7等。
2、运用乘法分配律进行简算,遇到除以一个数,先化为乘以一个数的倒数,再分配。
如:2.5×(100+0.4),还应注意,有些题目是运用分配律的逆运算来简算:即提取公因数。如:0.93×67+33×0.93。
用简便方法计算: 101x99x999+999
101x99x999+999可以简便地计算为(100x100x100-1) + 999,即1000000-1+999,最终结果为1000997。这是因为当计算a乘以b再加上c时,如果a和b之间的差距较小,可以通过将其中一个数加上差值,再减去差值乘以另一个数的方法进行简化计算。
用简便方法计算: 101x99x999+999
我们可以使用近似计算的方法来计算这个表达式。
首先,我们可以将 101x99x999 近似为 100x100x1000,因为这三个数非常接近这些值。
然后,我们可以将 100x100x1000 简化为 10^2 x 10^2 x 10^3,利用指数幂的性质,我们可以得到 10^(2+2+3) = 10^7。
最后,我们将这个结果与 999 相加,即 10^7 + 999 = 10,000,999。
因此,101x99x999+999 的近似计算结果为 10,000,999。
