真包含包含区别

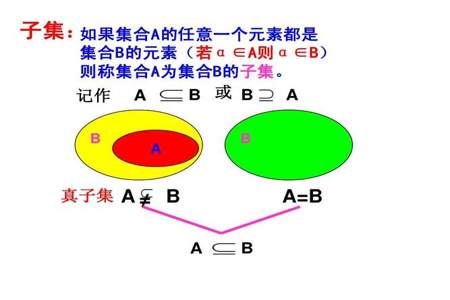
真包含和包含的区别就是在于包含的范围不同。

2、包含和真包含是集合与集合之间的关系，也叫子集和真子集关系。

3、真包含首先是包含（前一集合的元素都是后一集合的元素）但后一集合存在不是前一集合的元素。

包含就是包括（可以等同）。更广义一些。

真包含就是包括且不等同。

比如集合A={1,2,3,4} B={1,2} C={1,2,3,4}

就可以说C包含A,B.且 C真包含B.

真包含包含区别

“真包含”是数学中的一个概念，指一个集合B完全包含另一个集合A，即A的所有元素都属于B。换句话说，B中的所有元素都来自A。

如需了解更多关于“真包含”和“包含”的区别，建议查阅数学书籍或询问数学老师。

真包含包含区别

"真包含"和"包含"是数学中的两个概念，它们的区别在于：

- "包含"是指一个集合包含另一个集合的所有元素，即一个集合是另一个集合的子集。例如，集合 A = {1, 2, 3}包含集合 B = {1, 2, 3, 4}。

- "真包含"是指一个集合不仅包含另一个集合的所有元素，而且其本身也是另一个集合的子集。例如，集合 A = {1, 2, 3}真包含集合 B = {1, 2, 3, 4}。

因此，"包含"是一种弱关系，而"真包含"是一种更强的关系。在数学中，这两个概念用于描述集合之间的关系，对于研究数学问题和证明定理非常重要。