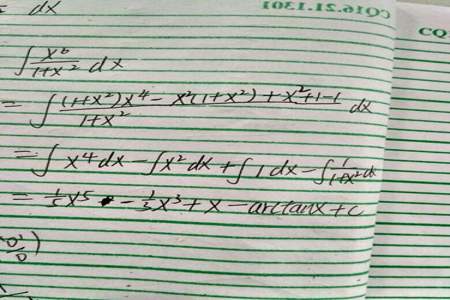
要求解函数 f(x) = x^2 + (1/x)^4 的积分,我们可以进行如下步骤:
将 f(x) = x^2 + (1/x)^4 展开变形,可以得到:
f(x) = x^2 + x^(-4)
将 x^(-4) 拆分为 (1/x^2)^2,可以进一步得到:
f(x) = x^2 + (1/x^2)^2
我们可以对 f(x) = x^2 + (1/x^2)^2 分别求积分,再将结果相加。
对于第一项 x^2,它的积分是 x^3/3。
对于第二项 (1/x^2)^2 = 1/x^4,我们可以使用换元法。
令 u = x^(-2), 则 du = -2x^(-3)dx,可以得到:
积分(1/x^4)dx = 积分-2u^2 du = -2积分u^2 du = -2(u^3/3) = -2(x^(-2))^3/3 = -2/(3x^6)
将两个积分结果相加,最终的积分形式为:
积分(x^2 + (1/x^2)^2)dx = x^3/3 - 2/(3x^6) + C
其中,C为积分常数。
x的平方+1分之x的四次方求积分
x的平方+1分之x的四次方的积分为
∫x^4/(1+x^2)dx
=∫(x^4-1+1)/(1+x^2)dx
=∫x^2dx-∫dx+∫1/(1+x^2)dx
=x^3/3-x+arctanx+C
